PERT - Program Evaluation and Review Technique
When you plan a project, you need to know exactly what's involved and how much time each component requires; the Program Evaluation and Review Technique, or PERT, can help you minimize the guesswork and manage your projects more efficiently. [By Lea Terry]
PERT (Program Evaluation and Review Techniques) chart is a flow chart or time chart that depicts a series of tasks or activities in the order that such tasks should be done to achieve project goals. [Source]
CPM and PERT have been successfully used in many applications, including:
1. Scheduling construction projects such as office buildings, highways, and swimming pools.
2. Scheduling the movement of a 400-bed hospital from Portland, Oregon, to a suburban location.
3. Developing a countdown and “hold” procedure for the launching of space flights.
4. Installing a new computer system.
5. Designing and marketing a new product.
6. Completing a corporate merger.
7. Building a ship. [Operations Research by Wayne L. Winston]
Uses of PERT / Program Evaluation and Review Technique
With PERT chart it is possible to determine the critical path, which is the precise sequence of activities which must be completed on time or the project will be delayed.
You can use PERT to provide higher confidence levels for duration estimates that might be shaky. You can apply it to every task, to certain risky tasks, or to the critical paths tasks. [Source]. In short PERT helps to remove partiality (favoritism / discrimination) from time estimation.
PERT is used on projects where risks in calculating time durations have a high variability. [Source]
PERT is used on Projects where percent complete is almost impossible to determine except at completed milestones.[Source]
Advantages of PERT / Program Evaluation and Review Technique
PERT chart provides a general outlook on the entire project planning process. This allows you to coordinate a number of activity sequences at the same time in addition to foreseeing potential traps. PERT also determines where the large efforts should be made in order to keep the project on schedule.
PERT is applicable to a wide range of projects e.g. construction, software development, movie productions, building a ship etc.
PERT can determine the probability of meeting the deadlines by developing alternative plans.
PERT is a great decision making tool.
PERT can monitor costs also along with schedules.
Disadvantages of PERT / Program Evaluation and Review Technique
PERT requires too much of detail. Project activities need to be clearly defined, independent in their relationships.
The activity time estimates are to some extent subjective and depend on judgment & experience and sometimes subject to tampering by managers.
Directly PERT does not consider cost in project evaluation.
When to use PERT / Program Evaluation and Review Technique
Because it is primarily a project-management tools, a PERT chart is most useful for planning and tracking entire projects or for scheduling and tracking the implementation phase of a planning or improvement effort. [Source]
Steps to create a PERT / Program Evaluation and Review Technique chart
Generalized steps involved in PERT planning are:
1. Identify the specific activities and milestones.
2. Determine the proper sequence of the activities.
3. Construct a network diagram.
4. Estimate the time required for each activity.
5. Determine the critical path.
6. Update the PERT chart as the project progresses.
[Source]
Example of PERT
The RELIABLE CONSTRUCTION COMPANY has just made the winning bid of $5.4 million to construct a new plant for a major manufacturer. The manufacturer needs the plant to go into operation within a year. Therefore, the contract includes the following provisions:
A penalty of $300,000 if Reliable has not completed construction by the deadline 47 weeks from now.
To provide additional incentive for speedy construction, a bonus of $150,000 will be paid to Reliable if the plant is completed within 40 weeks.
Mr. Perty will need to arrange for a number of crews to perform the various construction activities at different times. Table (below) shows his list of the various activities. The third column provides important additional information for coordinating the scheduling of the crews.
For any given activity, its immediate predecessors (as given in the third column of below Table) are those activities that must be completed by no later than the starting time of the given activity. (Similarly, the given activity is called an immediate successor of each of its immediate predecessors.)
Table 1 of Activity list for the Reliable Construction Co. project
| Activity | Activity Description | Immediate Predecessors | Estimated Duration |
|---|---|---|---|
| A | Excavate | - | 2 weeks |
| B | Lay the foundation | A | 4 weeks |
| C | Put up the rough wall | B | 10 weeks |
| D | Put up the roof | C | 6 weeks |
| E | Install the exterior plumbing | C | 4 weeks |
| F | Install the interior plumbing | E | 5 weeks |
| G | Put up the exterior siding | D | 7 weeks |
| H | Do the exterior painting | E,G | 9 weeks |
| I | Do the electrical work | C | 7 weeks |
| J | Put up the wallboard | F, I | 8 weeks |
| K | Install the flooring | J | 4 weeks |
| L | Do the interior painting | J | 5 weeks |
| M | Install the exterior fixtures | H | 2 weeks |
| N | Install the interior fixtures | K,L | 6 weeks |
Given all the information in above Table, Mr. Perty now wants to develop answers to the following questions.
1. How can the project be displayed graphically to better visualize the flow of the activities?
2. What is the total time required to complete the project if no delays occur?
3. When do the individual activities need to start and finish (at the latest) to meet this project completion time?
4. When can the individual activities start and finish (at the earliest) if no delays occur?
5. Which are the critical bottleneck activities where any delays must be avoided to prevent delaying project completion?
6. For the other activities, how much delay can be tolerated without delaying project completion?
7. Given the uncertainties in accurately estimating activity durations, what is the probability of completing the project by the deadline?
Answer 1.

Fig 1
A network used to represent a project is called a project network. A project network consists of a number of nodes (typically shown as small circles or rectangles) and a number of arcs (shown as arrows) that lead from some node to another.
Three types of information are needed to describe a project.
1. Activity information: Break down the project into its individual activities (at the desired level of detail).
2. Precedence relationships: Identify the immediate predecessor(s) for each activity.
3. Time information: Estimate the duration of each activity.
The project network needs to convey all this information. Two alternative types of project networks are available for doing this:
activity-on-arc (AOA)
activity-on-node (AON) - we are using this here - where each activity is represented by a node. The arcs then are used just to show the precedence relationships between the activities. In particular, the node for each activity with immediate predecessors has an arc coming in from each of these predecessors.
Answer 2 to Answer 6.
A path through a project network is one of the routes following the arcs from the START node to the FINISH node. The length of a path is the sum of the (estimated) durations of the activities on the path.
The six paths through the project network are given below, along with the calculations of the lengths of these paths. The path lengths range from 31 weeks up to 44 weeks for the longest path (the fourth one in the table).
| Path | Length |
|---|---|
| Start ->A->B->C->D->G->H->M->FINISH | 2+4+10+6+7+9+2 = 40 weeks |
| Start ->A->B->C->E->H->M->FINISH | 2+4+10+4+9+2 = 31 weeks |
| Start ->A->B->C->E->F->J->K->N->FINISH | 2+4+10+4+5+8+4+6 = 43 weeks |
| Start ->A->B->C->E->F->J->L->N->FINISH | 2+4+10+4+5+8+5+6 = 44 weeks |
| Start ->A->B->C->I->J->K->N->FINISH | 2+4+10+7+8+4+6 = 41 weeks |
| Start ->A->B->C->I->J->L->N->FINISH | 2+4+10+7+8+5+6 = 42 weeks |
The (estimated) project duration equals the length of the longest path through the project network. This longest path is called the critical path. (If more than one path tie for the longest, they all are critical paths.)
Critical path: START ->A->B->C->E->F->J->L->N-> FINISH
(Estimated) project duration = 44 weeks.
If no delays occur, the total time required to complete the project should be about 44 weeks.
The activities on this critical path are the critical bottleneck activities where any delays in their completion must be avoided to prevent delaying project completion.
The starting and finishing times of each activity if no delays occur anywhere in the project are called the earliest start time and the earliest finish time of the activity.
ES = earliest start time for a particular activity,
EF = earliest finish time for a particular activity,
where
EF =ES + (estimated) duration of the activity.
Starting time for project = 0.
Activity A: ES = 0,
EF = 0 + duration (2 weeks)
= 2
Activity B: ES = EF for activity A
= 2,
EF = 2 + duration (4 weeks)
= 6.
If an activity has only a single immediate predecessor, then ES for the activity = EF for the immediate predecessor.
Activity C: ES = EF for activity B
= 6,
EF = 6 + duration (10 weeks)
= 16.
Activity D: ES = EF for activity C
= 16,
EF = 16 + duration (4 weeks)
= 20.
Now consider activity H, which has two immediate predecessors, activities G and E. Activity H must wait to start until both activities G and E are finished, which gives the following calculation.
Immediate predecessors of activity H:
Activity G has EF = 29.
Activity E has EF = 20.
Larger EF = 29.
Therefore,
ES for activity H = larger EF above
= 29.
Immediate predecessors of the FINISH node:
Activity M has EF = 40.
Activity N has EF = 44.
Larger EF = 44.
Therefore,
ES for the FINISH node = larger EF above
= 44.
EF for the FINISH node = 44 + 0 = 44.
This process of starting with the initial activities and working forward in time toward the final activities to calculate all the ES and EF values is referred to as making a forward pass through the network.

Fig - 2
Keep in mind that the schedule obtained from this procedure assumes that the actual duration of each activity will turn out to be the same as its estimated duration. What happens if some activity takes longer than expected? Would this delay project completion? Perhaps, but not necessarily. It depends on which activity and the length of the delay. The next part of the procedure focuses on determining how much later than indicated. In above Figure can an activity start or finish without delaying project completion.
The latest start time for an activity is the latest possible time that it can start without delaying the completion of the project (so the FINISH node still is reached at its earliest finish time), assuming no subsequent delays in the project. The latest finish time has the corresponding definition with respect to finishing the activity.
LS = latest start time for a particular activity,
LF = latest finish time for a particular activity,
where
LS = LF - (estimated) duration of the activity.
To find LF, we have the following rule.
The latest finish time of an activity is equal to the smallest of the latest start times of its immediate successors. In symbols,
LF = smallest LS of the immediate successors.
FINISH node: LF = its EF = 44,
LS = 44 - 0 = 44.
Activity M: LF = LS for the FINISH node
= 44,
LS = 44 - duration (2 weeks)
= 42
Since activity M is one of the activities that together complete the project, we also could have automatically set its LF equal to the earliest finish time of the FINISH node without applying the latest finish time rule.
Since activity M is the only immediate successor of activity H, we now can apply the latest finish time rule to the latter activity.
Activity H: LF = LS for activity M
= 42,
LS = 42 - duration (9 weeks)
= 33.
Note that the procedure being illustrated above is to start with the final activities and work backward in time toward the initial activities to calculate all the LF and LS values. Thus, in contrast to the forward pass used to find earliest start and finish times, we now are making a backward pass through the network.
Below Figure shows the results of making a backward pass to its completion.
If the start and finish times in below figure for a particular activity are later than the corresponding earliest times in above Figure, then this activity has some slack in the schedule. The last part of the PERT/CPM procedure for scheduling a project is to identify this slack, and then to use this information to find the critical path.

Fig - 3

Fig - 4
The slack for an activity is the difference between its latest finish time and its earliest finish time. In symbols,
Slack = LF - EF.
(Since LF - EF = LS - ES, either difference actually can be used to calculate slack.)
For example,
Slack for activity M = 44 - 40 = 4.
This indicates that activity M can be delayed up to 4 weeks beyond the earliest time schedule without delaying the completion of the project at 44 weeks.
Note that some of the activities have zero slack, indicating that any delays in these activities will delay project completion.
This is how PERT/CPM identifies the critical path(s).
| Activity | Slack(LF-EF) | On Critical Path? |
|---|---|---|
| A | 0 | Yes |
| B | 0 | Yes |
| C | 0 | Yes |
| D | 4 | No |
| E | 0 | Yes |
| F | 0 | Yes |
| G | 4 | No |
| H | 4 | No |
| I | 2 | No |
| J | 0 | Yes |
| K | 1 | No |
| L | 0 | Yes |
| M | 4 | No |
| N | 0 | Yes |
Thus, the critical path is
START ->A->B->C->E->F->J->L->N-> FINISH
Question 2: What is the total time required to complete the project if no delays occur? This is the earliest finish time at the FINISH node (EF = 44 weeks)
Question 3: When do the individual activities need to start and finish (at the latest) to meet this project completion time? These times are the latest start times (LS) and latest finish times (LF) given in Figs. 3 and 4. These times provide a "last chance schedule" to complete the project in 44 weeks if no further delays occur.
Question 4: When can the individual activities start and finish (at the earliest) if no delays occur? These times are the earliest start times (ES) and earliest finish times (EF) given in Figs. 2 and 4. These times usually are used to establish the initial schedule for the project. (Subsequent delays may force later adjustments in the schedule.)
Question 5: Which are the critical bottleneck activities where any delays must be avoided to prevent delaying project completion? These are the activities on the critical path shown by the darker arrows in Fig. 4. Mr. Perty needs to focus most of his attention on keeping these particular activities on schedule in striving to keep the overall project on schedule.
Question 6: For the other activities, how much delay can be tolerated without delaying project completion? These tolerable delays are the positive slacks given in the middle column of above Table.
Answer 7.
The three estimates to be obtained for each activity are
Most likely estimate (m) = estimate of the most likely value of the duration,
Optimistic estimate (o) = estimate of the duration under the most favorable conditions,
Pessimistic estimate (p) = estimate of the duration under the most unfavorable conditions.
Below is Variance:

Below is Mean:

The last two columns in the below table show the approximate mean and variance of the duration of each activity, as calculated from the above formulas. In this example, all the means happen to be the same as the estimated duration obtained in Table 1. Therefore, if all the activity durations were to equal their means, the duration of the project still would be 44 weeks, so 3 weeks before the deadline.
However, this piece of information is not very reassuring to Mr. Perty. He knows that the durations fluctuate around their means. Consequently, it is inevitable that the duration of some activities will be larger than the mean, perhaps even nearly as large as the pessimistic estimate, which could greatly delay the project.
To check the worst case scenario, Mr. Perty reexamines the project network with the duration of each activity set equal to the pessimistic estimate (as given in the fourth column of Table 2). Table 3 shows the six paths through this network and the length of each path using the pessimistic estimates. The fourth path, which was the critical path earlier, now has increased its length from 44 weeks to 69 weeks. However, the length of the first path, which originally was 40 weeks, now has increased all the way up to 70 weeks. Since this is the longest path, it is the critical path with pessimistic estimates, which would give a project duration of 70 weeks.
Given this dire (albeit unlikely) worst case scenario, Mr. Perty realizes that it is far from certain that the deadline of 47 weeks will be met. But what is the probability of doing so? PERT/CPM makes three simplifying approximations to help calculate this probability.
Table 2

Table 3
| Path | Length |
|---|---|
| Start ->A->B->C->D->G->H->M->FINISH | 3+8+18+10+11+17+3 = 70 weeks |
| Start ->A->B->C->E->H->M->FINISH | 3+8+18+5+17+3 = 54 weeks |
| Start ->A->B->C->E->F->J->K->N->FINISH | 3+8+18+5+10+9+4+9 = 66 weeks |
| Start ->A->B->C->E->F->J->L->N->FINISH | 3+8+18+5+10+9+7+9 = 69 weeks |
| Start ->A->B->C->I->J->K->N->FINISH | 3+8+18+9+9+4+9 = 60 weeks |
| Start ->A->B->C->I->J->L->N->FINISH | 3+8+18+9+9+7+9 = 63 weeks |
Probability Distribution of Project Duration.
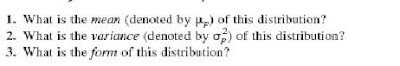
The mean critical path is the path through the project network that would be the critical path if the duration of each activity equals its mean.
Reliable’s mean critical path is START->A->B->C->E->F->J->L->N->FINISH,
As highlighted in Fig 4
Simplifying Approximation 1: Assume that the mean critical path will turn out to be the longest path through the project network. This is only a rough approximation, since the assumption occasionally does not hold in the usual case where some of the activity durations do not equal their means. Fortunately, when the assumption does not hold, the true longest path commonly is not much longer than the mean critical path (as illustrated in Table 3).

2.
Simplifying Approximation 2: Assume that the durations of the activities on the mean critical path are statistically independent. This assumption should hold if the activities are performed truly independently of each other. However, the assumption becomes only a rough approximation if the circumstances that cause the duration of one activity to deviate from its mean also tend to cause similar deviations for some other activities.


Since the means and variances of the durations for all the activities of Reliable’s project already are given in Table 2, we only need to record these values for the activities on the mean critical path as shown in below table. Summing the second column and then summing the third column give


Now we just need an approximation for the form of the probability distribution of project duration.
Simplifying Approximation 3: Assume that the form of the probability distribution of project duration is a normal distribution, as shown in below fig. By using simplifying approximations 1 and 2, one version of the central limit theorem justifies this assumption as being a reasonable approximation if the number of activities on the mean critical path is not too small (say, at least 5). The approximation becomes better as this number of activities increases. Now we are ready to determine (approximately) the probability of completing Reliable’s project within 47 weeks.


Therefore, using Table (or Table)for a standard normal distribution (a normal distribution with mean 0 and variance 1), the probability of meeting the deadline (given the three simplifying approximations) is

If you want to have more complete and detailed look at the above example then you can go for this book.
A couple of more documents on PERT
PERT Practice
A PERT example